A cura di Matteo Vettori
Il metodo agli elementi finiti è un approccio numerico per ottenere soluzioni approssimate ai problemi descritti da equazioni alle derivate parziali. Viene ampiamente utilizzato nell’ingegneria e in altri campi per analizzare strutture e sistemi fisici complessi.
Il metodo comporta la suddivisione dell’area o del volume in esame in elementi di dimensioni ragionevoli, connessi tramite nodi comuni. Ogni elemento viene approssimato utilizzando una funzione che soddisfa le equazioni differenziali nell’elemento stesso. Connettendo tutti gli elementi insieme, si ottiene una soluzione approssimata per l’intera struttura. Una maglia con elementi più piccoli può migliorare la precisione della soluzione, a scapito di un maggior onere computazionale.
Il metodo degli elementi finiti comporta le seguenti fasi:
1. Discretizzare i corpi del modello (le parti meccaniche) in elementi finiti.
In altre parole, si tratta di generare la griglia di calcolo.
Gli elementi più comunemente utilizzati sono aste (1D), triangoli o rettangoli (2D) e tetraedri o esaedri (3D).
L’insieme degli elementi adiacenti, facenti parte dello stesso corpo, sono uniti fra di loro attraverso i nodi, che vengono condivisi da elementi ad elemento ed attraverso i quali gli elementi si passano le forze.
Ogni elemento ha la sua funziona di forma, normalmente un polinomio di primo o di secondo grado, continue all’interno dell’elemento. Ad ogni elemento finito devono poi essere associate le proprietà fisiche corrispondenti, un set di informazioni che completano la descrizione dell’elemento, tra le quali è sempre presente il modello di materiale e le relative proprietà meccaniche.
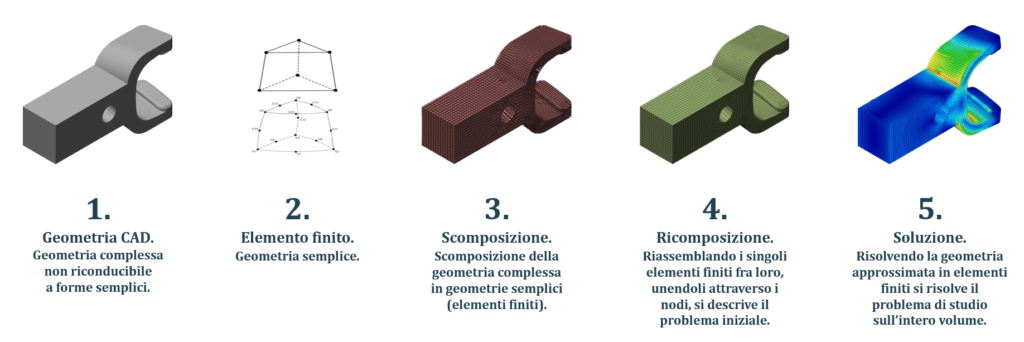
Il trucco matematico alla base del metodo agli elementi finiti è quello di descrivere la geometria continua dell’oggetto da studiare in un insieme di geometrie semplici nelle quali è possibile risolvere il problema. L’insieme delle geometrie semplici approssima la geometria iniziale e permette di risolvere il problema..
2. Assegnare Carichi e Vincoli al modello.
Stiamo parlando della cosiddetta schematizzazione del problema da risolvere.
Ai nodi di contorno, appartenenti alla superficie esterna dei corpi descritti dagli elementi finiti, si applicano le forze esterne, ed i vincoli di spostamento che vanno a limitare i gradi di libertà dei nodi (i possibili movimenti dei nodi). Carichi di pressione possono essere assegnati alle facce esterne degli elementi finiti e carichi di campo come accelerazioni possono essere applicate all’interno modello.
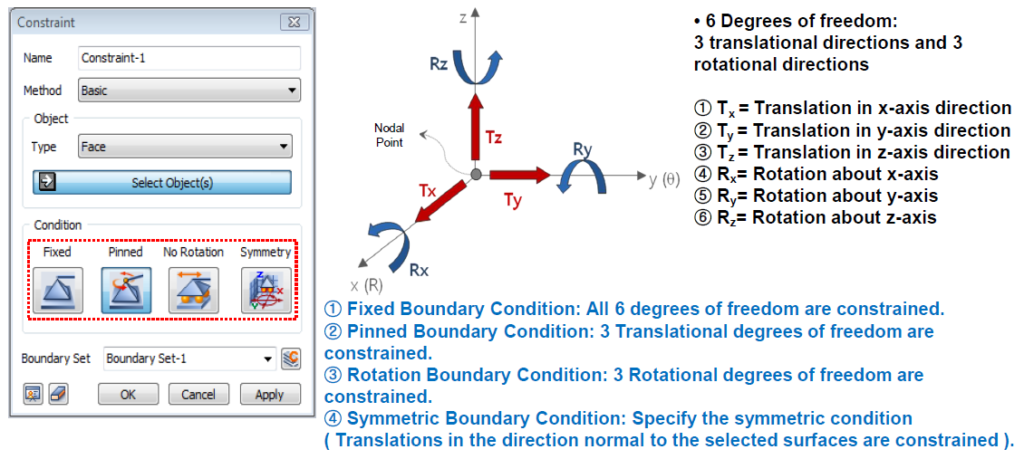
Vincolare un modello FEM significa vincolare i suoi nodi andando a limitare i loro gradi di libertà, ovvero i loro spostamenti possibili. midas NFX implementa comandi di vincolo pre-configurati oppure permette di combinare a piacere nodo per nodo le limitazioni di spostamento.
ATTENZIONE !
Non tutti gli elementi hanno 6 gradi di libertà ai nodi.
Gli elementi solidi ne hanno solo 3, per questo quando si collegano elementi 1-D e 2-D ad elementi solidi è possibile si generino delle labilità del modello (modello non completamente vincolato) e non tutte le azioni vengano correttamente trasmesse tra le due tipologie di elemento.
3. Risolvere il problema.
Questo è lavoro del solutore. Ma cosa succede da quando si da il comando “run” a quando si visualizzano i risultati?
Il modello ad elementi finiti, formato da mesh, carichi e vincoli viene normalmente tradotto in un “file di input” che è passato al solutore per la soluzione. Il solutore legge il modello e per ogni elemento genera la corrispondente matrice di rigidezza, l’insieme delle quali è poi assemblato nella matrice di rigidezza del modello che rappresenta il sistema di equazioni globali che descrivono il problema da risolvere.
Il modello FEM che a monitor vediamo come una rappresentazione più o meno fedele di un assieme meccanico con carichi e vincoli applicati a questo punto ha assunto le sembianze di un sistema di equazioni rappresentato in forma matriciale.
Per una analisi strutturale Forza-spostamenti ad esempio il sistema matriciale ha la forma
F = [ K ] * s ,
dove:
[ K ] – è la matrice del problema ad elementi finiti;
( s ) – il vettore degli spostamenti
( F ) – vettore delle forze
Risolvere il problema è a questo punto individuare le incognite del problema, il campo degli spostamenti ed il campo delle forze interne che si scambiano gli elementi fra di loro.
Una volta che il campo degli spostamenti nodali è noto su ogni elemento è dunque possibile calcolarsi le grandezze caratteristiche che si vogliono conoscere quali ad esempio la tensione e la deformazione. Queste grandezze sono calcolate con esattezza in punti specifici dell’elemento (punti di integrazione) attraverso integrazione numerica e poi “spalmate” su tutto l’elemento utilizzando le funzionai di forma che per ogni punto di integrazione (i) rappresentano il peso dal parametro calcolato in (i) nella generica posizione (x,y,z) all’interno dell’elememto. In altre parole, il valore del dato parametro nel generico punto (x,y,z) è la media pesata attraverso le funzioni di forma dell’elemento del valore del parametro calcolato negli n punti di integrazione dell’elememto.
Ed ecco che .. una volta completata questa nuova fase di calcolo all’interno di ogni elemento il calcolo è completato ed i risultati sono pronti per la visualizzazione.
4. Post-processing o analisi dei risultati.
Un calcolo ad elementi finiti non termina semplicemente con la produzione dei risultati (..quando finalmente la ventola del processore smette di sventolare), dopo il calcolo inizia la seconda parte del lavoro per l’utente, interpretare i risultati alla luce delle scelte fatte nella generazione del modello.
Ogni software mette a disposizione funzionai base di visualizzazione e analisi dei risultati (contour plot e deformata), i software completi le integrano con visualizzazioni avanzate (vettoriali, iso-linee, iso-superfici, visualizzazioni a soglia, …).
Oltre alle visualizzazioni è importante poter interrogare i dati a monitor (probe) o ad esempio poter controllare come i risultati vengono mediati e “omogeneizzati” tra elemento ed elemento.
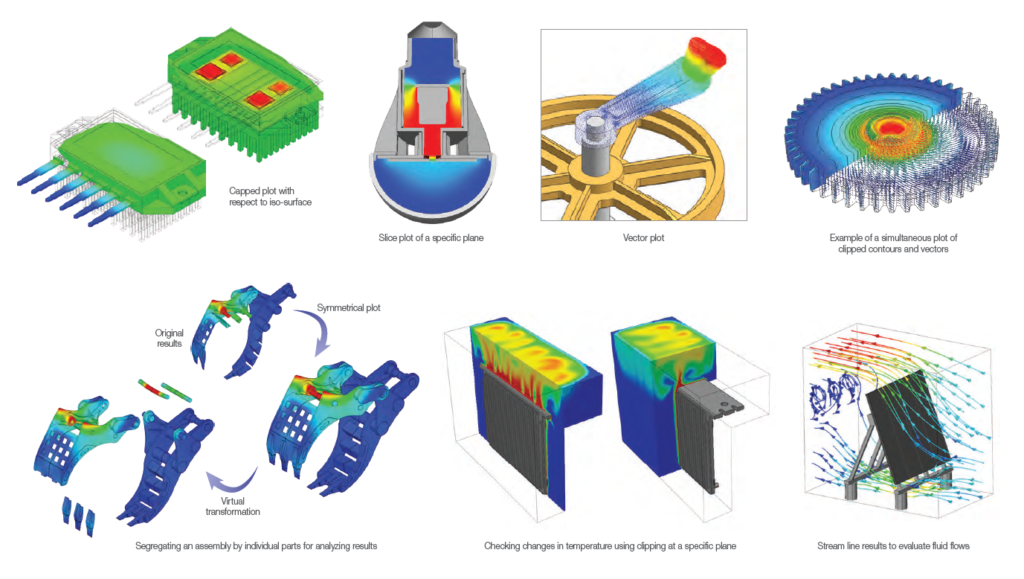
Alcuni esempi delle funzioni di post-processing avanzato presenti in midas NFX.
I software di modellazione ad elementi finiti professionali affiancano alle funzionai di post-processing di base, comandi grafici avanzati per interpretare meglio i risultati di una analisi.
ATTENZIONE !
Ricorda che il risultato di un calcolo, proprio perché è fatto in pochi punti all’interno di un elemento e interpolato all’interno dell’elemneto stesso, non è continuo tra elemento ed elemento. Il post-processore quando visualizza il contour-plot di una grandezza come la tensione realizza una ulteriore approssimazione dei risultati numerici andando ad eliminare le discontinuità tra elemento ed elemento (inter-element jumps).
Ora che abbiamo dettagliato le sue fasi .. quali sono i vantaggi del metodo ad elementi finiti?
Il metodo degli elementi finiti converte un problema differenziale definito continuamente in un problema algebrico, che può essere risolto numericamente da un computer. Ciò consente di ottenere soluzioni approssimate ma sufficientemente accurate per la maggior parte delle applicazioni ingegneristiche.
