Ottimizzazione topologica, il settimo senso del progettista.

L’ottimizzazione topologica rivoluziona la progettazione di componenti leggeri e performanti. Immagina una staffa in lamiera: attraverso algoritmi sofisticati, rimuoviamo il materiale superfluo, massimizzando l’efficienza senza compromettere la resistenza. In questo articolo esploriamo i concetti i concetti di base ed i vantaggi di questa tecnica, oltre a presentarti gli strumenti software per iniziare. Scopri come trasformare il design tradizionale in un’arte dell’efficienza .

Nuovo portale del supporto tecnico

Con l’obiettivo di fornire una migliore esperienza d’uso e una maggiore semplicità, è stato avviato il processo di semplificazione ed unificazione dei vari account e delle relative procedure di autenticazione ai portali ed ai prodotti MIDASIT. Scopri cosa cambia.

Design-by-Analysis più efficiente con l’Ottimizzazione Topologica

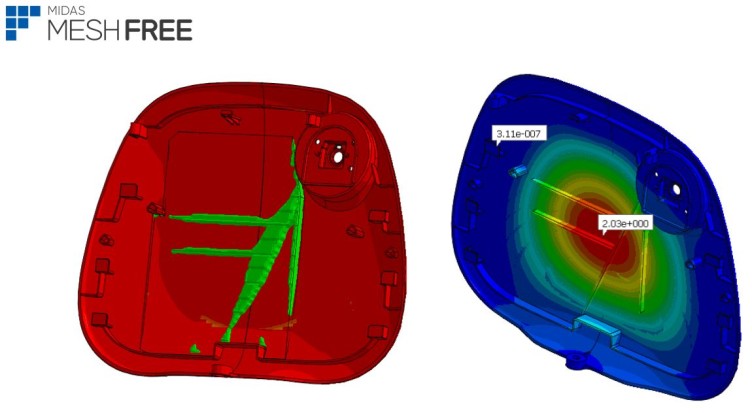
L’utilizzo intelligente dell’Ottimizzazione Topologica rende il tradizionale approccio di Design-by-Analysis più efficacie.
Attraverso l’esempio di un casing plastico per apparecchio medico, l’ottimizzazione topologica ha rivelato soluzioni non intuitive, permettendo minor tempo di sviluppo e minor impiego di materiale.

Prevedere le deformazioni in uno stampo

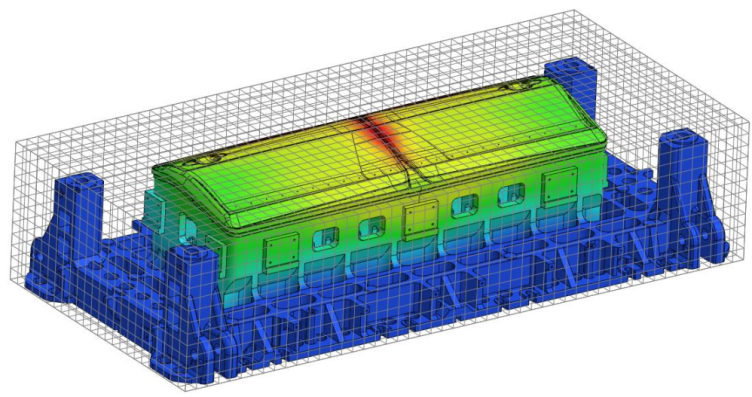
I repentini cambiamenti nel design automobilistico stanno riducendo ulteriormente i tempi di produzione. In questo processo, è necessario effettuare un’ottimizzazione rapida del design per la deformazione dello stampo.

Il lato sensibile del FEM

L’ingegnere naviga tra dettagli e ipotesi, specialmente nell’analisi agli elementi finiti. Questo articolo esplora l’importanza dell’analisi di “sensitività” in un caso pratico legato al basamento di una macchina per il packaging. Scopri come diverse condizioni di vincolo influenzano i risultati strutturali e come uno studio di sensitività può illuminare le scelte di modellazione.

Introduzione al FEM

Il Metodo agli Elementi Finiti (FEM) è un approccio numerico utilizzato in ingegneria e altri campi per risolvere problemi descritti da equazioni alle derivate parziali. Si suddivide l’area o il volume in elementi connessi da nodi, ciascuno approssimato da una funzione. Carichi e vincoli vengono assegnati ai nodi di contorno, mentre il solutore risolve il problema trasformando il modello in un sistema di equazioni globali. Dopo il calcolo, il post-processing analizza i risultati e li visualizza in varie forme. L’FEM è un potente strumento per analizzare strutture complesse, ma richiede scelte di modellazione e interpretazione accurata dei risultati.